Estimación de la constante de Hubble a partir de señales de las oscilaciones acústicas bariónicas con datos simulados del LSST

• Autor invitado: Miguel Antonio Sabogal Garcia

Miguel A. Sabogal García es egresado del programa de física de la Universidad del Atlántico (Colombia). Miguel realizó la investigación que se resume a continuación como parte del Red de Estudiantes Colombianos de Astronomía (RECA) Internship Program 2022 bajo la supervisión del Dr. Javier Gonzalez de la Universidade Federal de Sergipe (Brazil). Estos resultados preliminares de esta investigación se presentaron en el Simposio RECA Internship 2022.

Las investigaciones en cosmología a lo largo de la historia nos han conducido al actual modelo cosmológico estándar, 𝛬CDM (por sus siglas en ingles), en el que CDM se refiere a la materia oscura fría (materia que no interactúa con la radiación electromagnética y no posee presión) y 𝛬 corresponde a la famosa constante cosmológica de Einstein. Este término 𝛬 es el candidato más sencillo para representar la energía oscura que causa la expansión acelerada del universo, como indican varias observaciones astronómicas de supernovas, oscilaciones acústicas bariónicas, anisotropías de la radiación cósmica de fondo (CMB, por sus siglas en ingles), cronómetros cósmicos, entre otras. Sin embargo, a pesar de ser consistente con los datos cosmológicos actuales, el fuerte avance en la precisión de la cosmología ha desvelado que 𝛬CDM presenta inconsistencias como el problema de la tensión en el valor actual del parámetro de Hubble (H₀).  En este astrobito, que resume un práctica investigativa, se aborda este problema observacional: la tensión actual en los valores medidos de H_0. La tensión surge porque al asumir el modelo 𝛬CDM en el análisis de los datos del CMB se obtiene un valor de H₀ =67.4 ± (0.5) km/s/Mpc (Planck 2018), mientras que la combinación de las mediciones locales independientes de modelos estima H₀ =73.04+-(1.4) km s^-1 Mpc^-1 , valor que se encuentra en una tensión ~5𝜎 con las restricciones del CMB.

¿Qué otro fenómeno físico permite medir H₀?

Uno de los muchos fenómenos físicos que permiten estimar el valor de H₀ son las Oscilaciones Acústicas de Bariones (BAO, por sus siglas en inglés). Este fenómeno se generó cuando en el fluido de fotón-plasma fuertemente acoplado antes de la recombinación, las ondas acústicas soportadas por la presión de los fotones crearon una escala característica conocida como Horizonte de sonido (R_s) en la distribución espacial del fluido. Tras el desacoplamiento barión-fotón, el horizonte de sonido se congeló pero siguió evolucionando gravitacionalmente en la distribución de materia, lo que puede observarse en las funciones de correlación posteriores de las galaxias. El horizonte de sonido durante la recombinación se puede determinar con precisión con el CMB, por lo que las BAO se convierten en una regla estándar muy importante para medir la distancia de diámetro angular, y estimar cantidades como el parámetro de Hubble y parámetros de densidad.

En la literatura se proponen constantemente modelos teóricos para estudiar la cosmología más allá de 𝛬CDM. Aunque este enfoque puede proporcionar restricciones estrictas sobre los parámetros cosmológicos, los resultados pueden estar sesgados hacia los modelos considerados. Una alternativa interesante y robusta es considerar un Proceso Gaussiano (PG), para reconstruir los parámetros cosmológicos de forma independiente del modelo. Esta alternativa se ha hecho especialmente popular en la última década.

En este trabajo aplicamos el método de reconstrucción no paramétrica PG a las señales BAO anisotrópicas simuladas del Large Synoptic Survey Telescope (LSST) para obtener una estimación de la incertidumbre de H₀ en una futura medición de BAO realizada por el LSST.

¿Qué son los Procesos Gaussianos?

Un proceso gaussiano es una colección de variables aleatorias que describe una distribución sobre funciones y, por tanto, son una generalización de las distribuciones gaussianas al espacio de funciones. Un PG permite realizar la reconstrucción de una función a partir de los datos, sin asumir una parametrización (modelo) de la función.

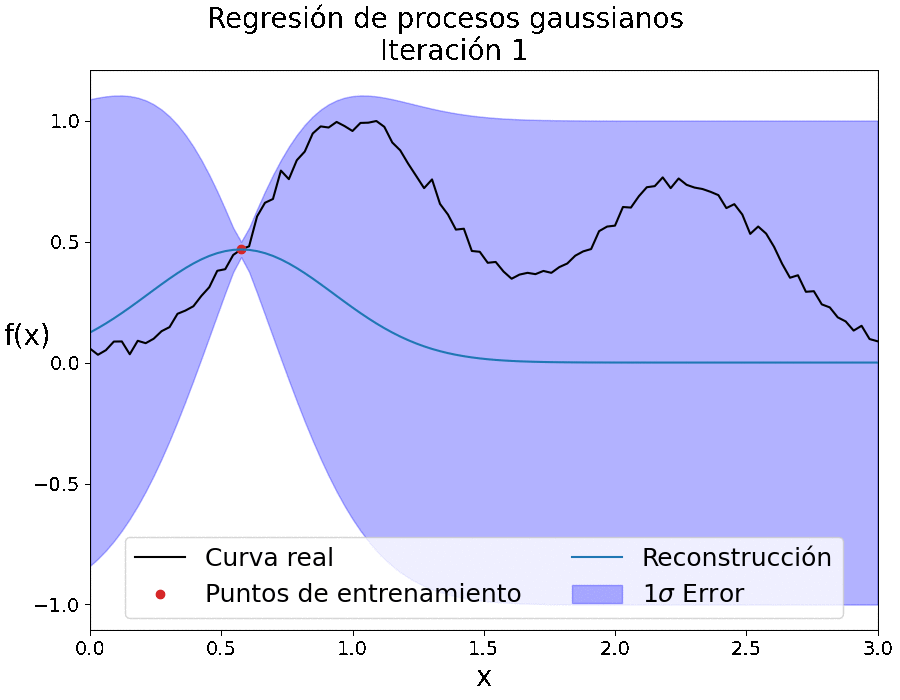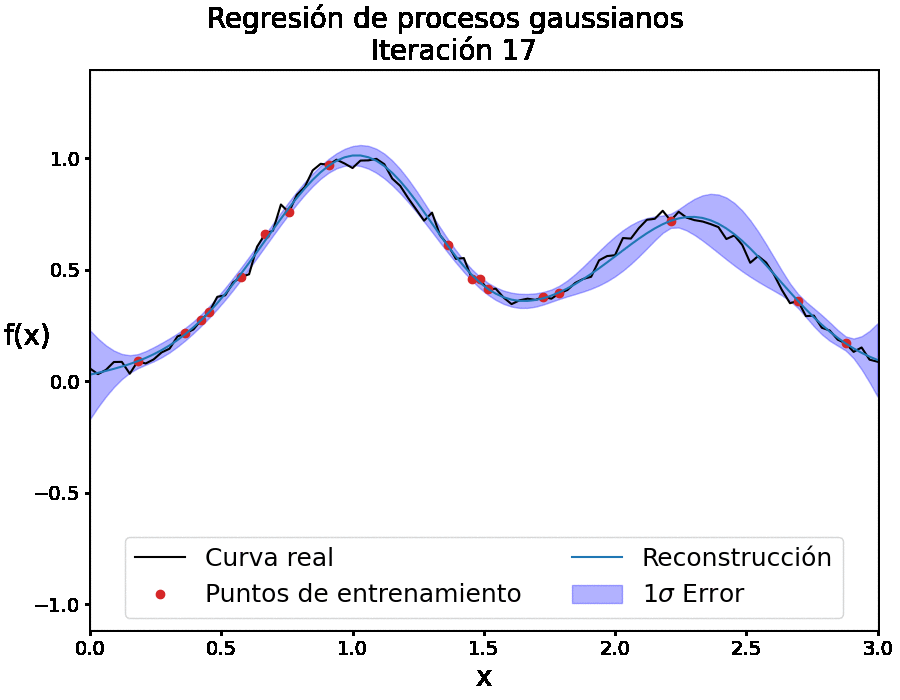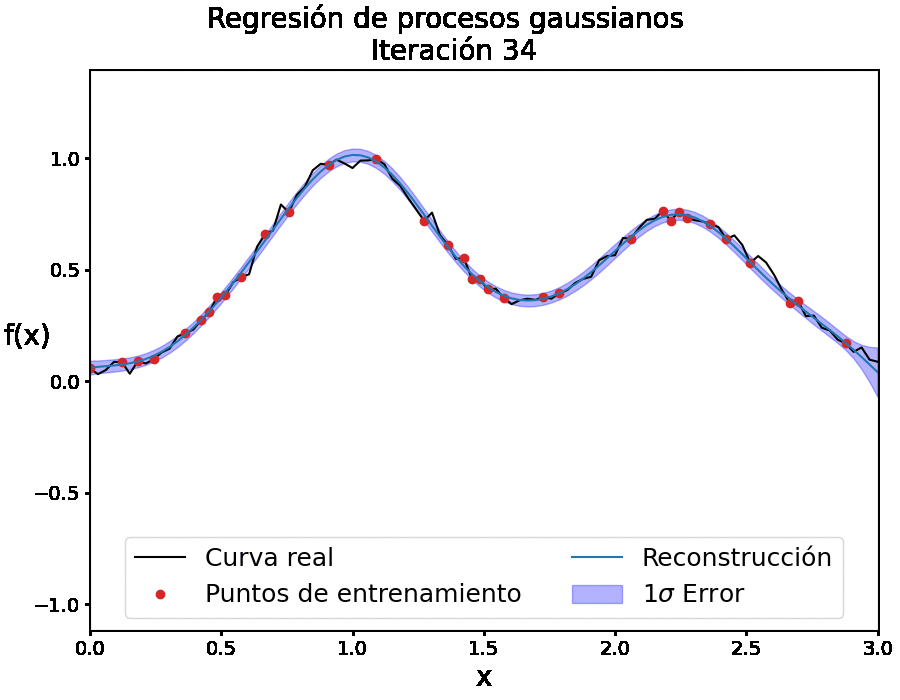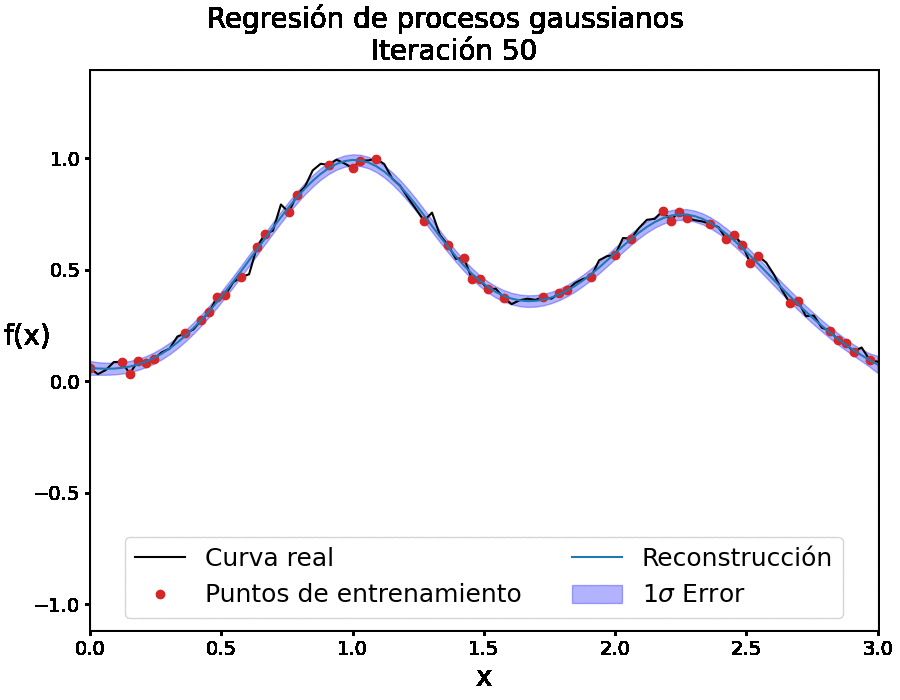
Para nuestro contexto, la idea principal de los PGs consiste en reconstruir una función f(x) que describa los datos (ver Figura 1). En este trabajo escribiremos el conjunto de puntos de entrenamiento, es decir, las ubicaciones {x_i}ⁿ_i=1 de las observaciones como X, y las ubicaciones en las que queremos reconstruir la función se denotan como X^*.

El valor de f cuando se evalúa en un punto x es una variable aleatoria gaussiana con media μ(x) y la varianza está relacionada con la función de covarianza cov(f(x),f(x̂))=k(x,x̂). Hay una amplia gama de posibles funciones de covarianza y para este trabajo hemos utilizado la función de covarianza denominada exponencial cuadrática. Esta función tiene la ventaja de que es infinitamente diferenciable, lo que resulta útil para reconstruir las derivadas de una función (también un proceso gaussiano). Otra característica aún más importante de la función exponencial cuadrática es su dependencia de dos parámetros ajustables (hiperparámetros) que permiten controlar el proceso de entrenamiento, 𝜎_f y ℓ, determinando la suavidad de la función reconstruida.

Al inicio del proceso los hiperparámetros son desconocidos. Estos hiperparámetros se pueden entrenar maximizando la probabilidad marginal, que es la marginalización sobre los valores de la función f en ubicaciones X. Es importante señalar que esta metodología sólo depende de las ubicaciones X de las observaciones, pero no de los puntos X^*, donde queremos reconstruir la función.

Para estimar la incertidumbre de H₀ en una medición futura de BAO por el LSST, se construyó una librería basada en el código GaPP, donde la distancia co-móvil D(z) y su derivada se reconstruyen a partir de los conjuntos de datos, con el fin de obtener H(z), siendo z el corrimiento al rojo.

El modelo fiducial para simular nuestro universo (los datos) puede elegirse entre las opciones 𝛬CDM, wCDM (el cual asume que la energía oscura tiene una ecuación de estado cosmológica constante (w) diferente a -1 (𝛬CDM), que es la razón entre la presión y la densidad de energía del universo) o el modelo holográfico de energía oscura (GO) de Granda-Oliveros (un modelo bajo el principio holográfico que asume un w no constante a lo largo de la historia del universo), siendo 𝛬CDM el modelo por defecto. En primer lugar, estudiamos el caso con 𝛬CDM como modelo fiducial con N=100 reconstrucciones, un muestreo aleatorio gaussian de N*=1000 valores y μ=0 (es decir, sin parametrización). En la izquierda superior de la Figura 2 podemos observar cómo se comportan las N reconstrucciones y a la derecha la reconstrucción final de H(z) con especial atención en z=0, es decir en el presente. También podemos observar en la parte superior derecha de la Figura 2 que la estimación de H₀ coincide dentro de 1𝜎 de confianza con el valor fijado para este universo simulado. 

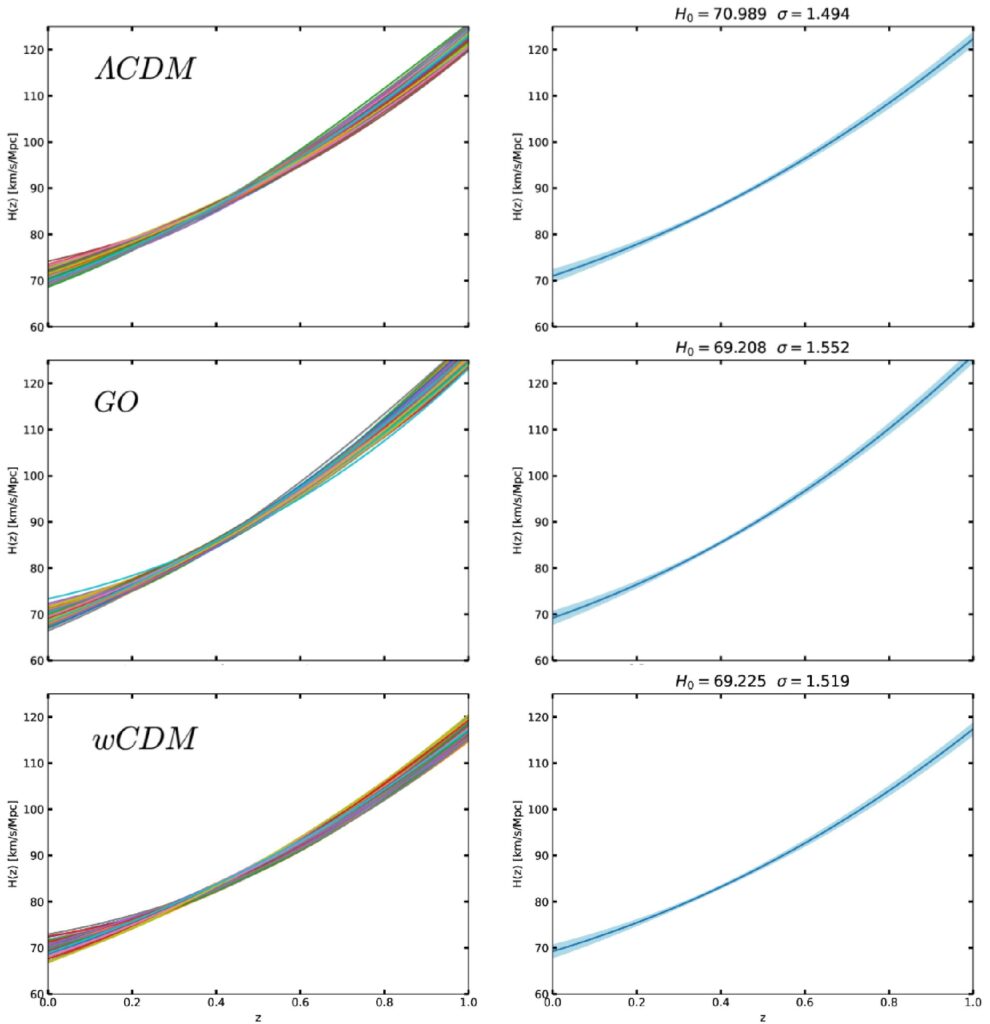
En segundo lugar, consideramos con las mismas condiciones anteriores a GO y wCDM como modelos fiduciales en la segunda y última fila de la Figura 2 respectivamente. Encontrando que por el método de la optimización los mejores resultados obtenidos (con menor incertidumbre) son cuando 𝛬CDM se considera como el modelo fiducial. No obstante, hay que señalar que en todos los casos se recupera el valor de H₀ del universo simulado, lo que pone de manifiesto la robustez de la metodología empleada.

En resumen,  en este trabajo hemos probado la posibilidad de aplicar el método de reconstrucción no paramétrico de Procesos Gaussianos a datos simulados a partir de señales BAO, generando una librería cuya metodología permite realizar la reconstrucción de parámetros cosmológicos como H(z) y D(z). Por último, a partir de los datos simulados del LSST, se estima que la incertidumbre de H₀ en una futura medición de BAO por el LSST tendría un valor menor a 𝜎=1.5 km/s/Mpc, lo que permitirá diferenciar entre los valores de la tensión actual hasta en 3.9𝜎 de confianza.

Esta investigación continúa, explorando el espacio de hiperparámetros utilizando el enfoque de marginalización mediante el método de cadenas Markov Monte Carlo (MCMC), debido a que el enfoque de optimización puede sobre-estimar los errores al no incluir otras combinaciones que den un buen ajuste a los datos.

Edición: Alejandro Cárdenas-Avendaño & Nicolas Garavito