Título del artículo técnico: Benford’s law in the GAIA universe
Autores: Jurjen de Jong, Jos de Bruijne, Joris De Ridder
Institución del primer autor: Science Support Oce, Directorate of Science, European Space Research and Technology Centre (ESA/ESTEC), Países Bajos.
Estado: Aceptado por Astronomy and Astrophysics [Acceso abierto]
Astrobite original: On stars, distances, and tax fraud por Laila Linke
Cuando los astrónomos llevan a cabo un gran sondeo, recolectan cantidades apabullantes de datos. Por supuesto, esto es algo bueno: más datos equivale a más información y, por tanto, mejor entendimiento de nuestro universo. Pero ¿cómo podemos saber si los datos son correctos? Bueno, los autores del artículo de hoy intentan usar una curiosidad matemática que generalmente se utiliza para detectar fraudes fiscales: la ley de Benford.
¿Qué es la ley de Benford?
La ley de Benford es un hecho matemático curioso. Dice que en un gran conjunto de datos, no todos los números tienen la misma probabilidad de aparecer. Un 30% de los datos debería empezar con 1, mientras que solo el 5% de los casos deberían comenzar con un 9. La figura 1 muestra la probabilidad de cada número entre 1 y 9 de ser el primer dígito de un dato.
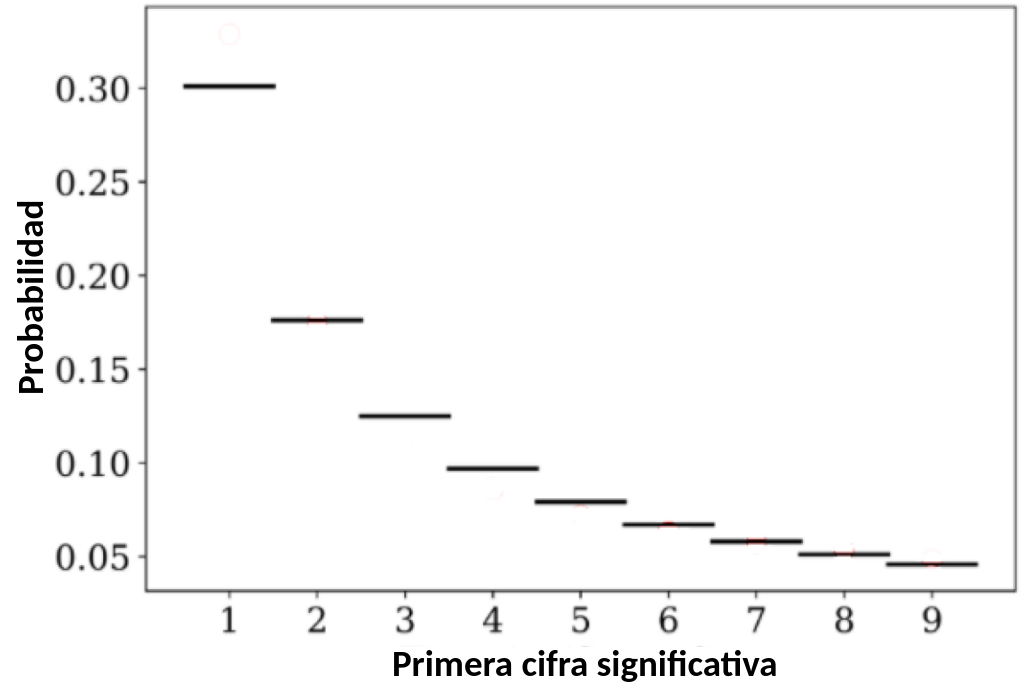
Esta ley parece bastante anti-intuitiva. Sin embargo, diferentes sets de datos la siguen — desde la bolsa de valores hasta las longitudes de los ríos. Una aplicación esencial de la ley de Benford es la detección de fraude fiscal. Cuando la gente se inventa números, frecuentemente eligen cada número entre 1 y 9 con la misma frecuencia — ignorando la ley de Benford. Por tanto, las declaraciones de impuestos que no siguen la ley de Benford podrían ser fraudulentas, es decir, los números que contienen podrían ser inventados. Similarmente, la ley de Benford ha sido utilizada para argumentar que los datos económicos enviados por Grecia a la Unión Europea antes de unirse a la Eurozona fueron manipulados.
Existen algunos prerrequisitos para que los datos sigan la ley de Benford. Primero, los datos no deberían estar truncados y deben distribuirse por varios órdenes de magnitud. Esto tiene sentido. Supongamos que todos los datos se distribuyen entre 5 y 8. Entonces la ley de Benford no podría cumplirse, ya que el número 1 no puede aparecer del todo. Segundo, los datos debería ser “invariantes de escala”. Esto significa que no debería haber ningún valor “importante” alrededor del cuál los datos se acumulen. Por ejemplo, si la mayoría de los datos tiene un valor cercano a 4, los dígitos 3, 4 y 5 aparecerán más frecuentemente que 1. Consecuentemente, no está claro desde el principio que un conjunto de datos particular cumpla la ley de Benford. Los autores del artículo de hoy estudian si podemos usarla para comprobar un conjunto de datos fascinante — las distancias a las estrellas en nuestra Vía Láctea.
¿Qué datos se analizan en el artículo de hoy?
Los autores estudian distancias estelares medidas por la misión Gaia. Gaia es un observatorio espacial, mostrado en la figura 2, con la tarea de crear el mapa más preciso de las estrellas en nuestra Vía Láctea hasta la fecha. Se planea que registre hasta mil millones de objetos, incluyendo principalmente estrellas, pero también planetas, cometas y asteroides (aprende más sobre Gaia en este astrobito).

Dado que Gaia quiere hacer un mapa de la Vía Láctea, sus observables principales son las posiciones y las distancias a las estrellas. Para estimar la distancia a una estrella, Gaia mide el así llamado efecto paralaje. Dado que la Tierra orbita alrededor del Sol, observamos una estrella en primavera bajo un ángulo ligeramente diferente que en otoño. Por tanto, su posición aparente en el cielo se desplaza. Este desplazamiento es llamado “el paralaje” y es inversamente proporcional a la distancia a la estrella. A partir de este paralaje, la distancia a la estrella puede ser estimada, teniendo en cuenta correcciones de sesgos sistemáticos e incertidumbres en las mediciones.
¿Siguen la ley de Benford los datos de Gaia?
La respuesta es un claro “Si y No”. La figura 3 muestra la distribución de los primeros dígitos de los paralajes de Gaia y la predicción de la ley de benford. Ambas distribuciones son bastante consistentes, por lo que la medida del paralaje parece seguir la ley matemática.
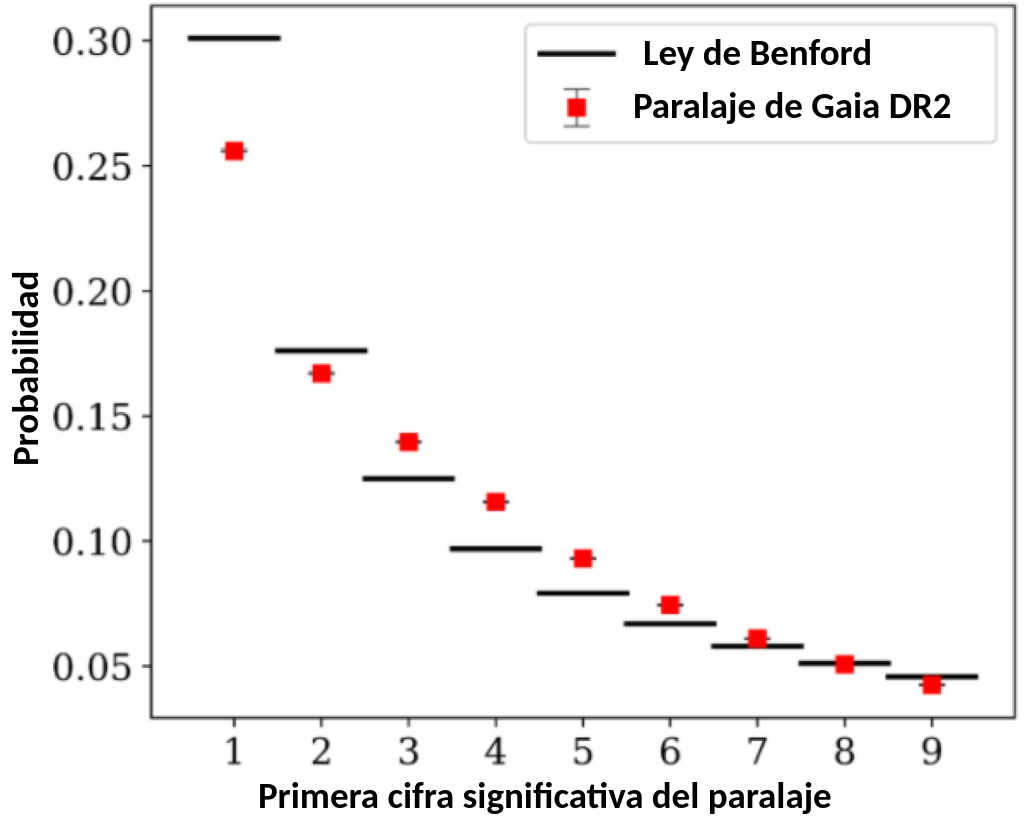
Sin embargo, la figura 4 pinta un cuadro diferente. Esta muestra la distribución del primer dígito de las distancias. La distribución tiene dos picos — uno en 1, y otro en 7. En consecuencia, las distancias estelares no están de acuerdo con la ley de Benford.
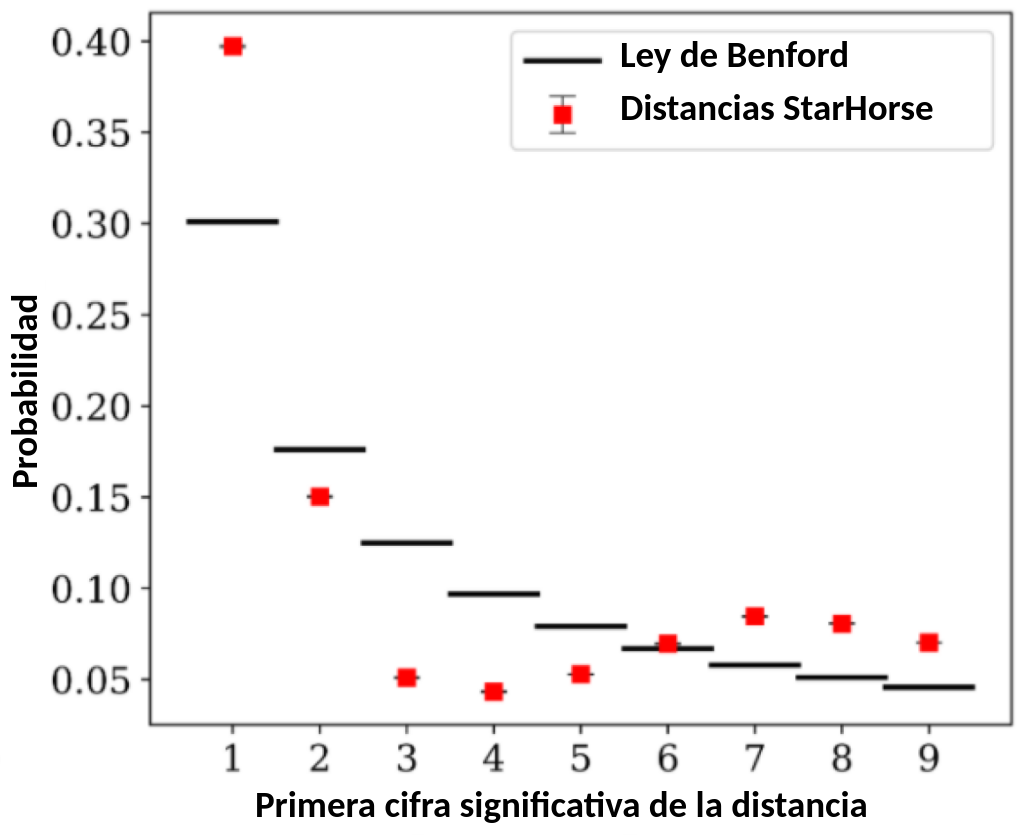
¿Significa esto que Gaia se equivoca?¿Necesitamos un nuevo satélite?
Bien, como explicamos arriba, no podemos aplicar la ley de Benford ciegamente a cualquier conjunto de datos. En particular, no debería haber ninguna escala “especial” en los datos. Para Gaia, sin embargo, hay una escala específica: el centro de la Vía Láctea está situado a unos 8 kpc de la Tierra, por lo que esperamos que muchas estrellas estén a distancias de entre 7 y 8 kpc. Además, hay solo unas pocas estrellas con distancias mayores a 10 kpc detectadas por Gaia, por lo que el conjunto de datos no se expande por varios órdenes de magnitud. Por lo tanto, la ley de Benford no es particularmente adecuada para este conjunto de datos.
Sin embargo, los paralajes medidos, se extienden en un rango de cuatro órdenes de magnitud — suficiente para aplicar la ley de Benford de un modo realista. Además los autores encontraron que al incrementar la incertidumbre en las medidas de paralaje lleva a un mejor acuerdo con la ley de Benford. Por tanto, las barras de error en las mediciones de paralaje podrían ser la razón por la que siguen la ley de Benford.
Los autores comprobaron si las distancias estelares deberían si acaso seguir la ley de Benford. Para esto, consideraron una simulación llamada Gaia Universe Model Snapshot (GUMS). Esta simulación es un model realista y sofisticado de la Vía Láctea. Para las estrellas de GUMS, todas las distancias desde el observador (osea, nosotros) son conocidas, así que los autores pudieron comprobar directamente si siguen o no la ley de Benford.
Su resultado se muestra en la figura 5. La simulación también exhibe un segundo pico en la distribución de los primeros dígitos. El segundo pico está alrededor de 6, similar al segundo pico observado en 7. Los autores concluyen que la ley de Benford no se aplica a mediciones de distancias estelares. Esta parece una conclusión poco satisfactoria, pero hay un reconfortante mensaje que podemos llevarnos del análisis: ¡las estrellas y la estructura de nuestra Vía Láctea son más complejas que los defraudadores!
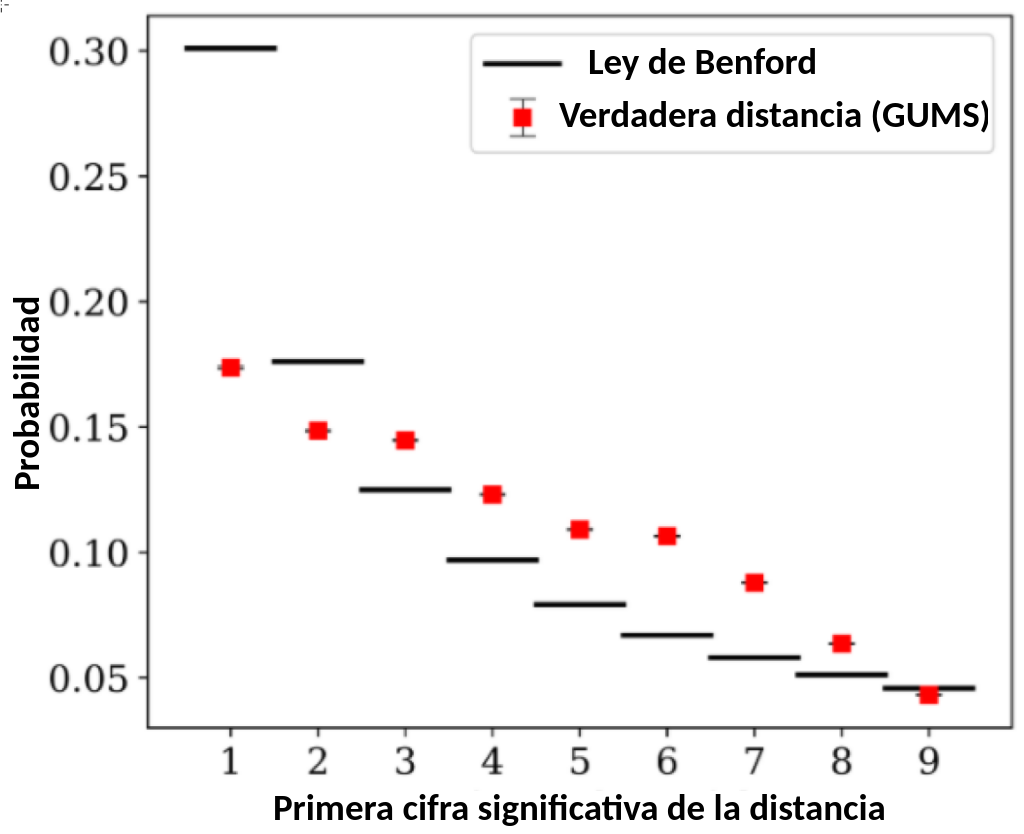
Astrobite original editado por Ashley Piccone.
Crédito de la imagen destacada: ESA/ATG medialab; fondo: ESO/S. Brunier
Comentarios
Aún no hay comentarios.