Equis ‘X’ marca la región

• Título del artículo: Hidden Worlds: Dynamical Architecture Predictions of Undetected Planets in Multi-planet Systems and Applications to TESS Systems
• Autores:  Jeremy Dietrich and Dániel Apai
• Institución del primer autor:  Departamento de Astronomía, Universidad de Arizona, Tucson
• Estado del artículo I: enviado a AJ, acceso abierto en arXiv
• Astrobite: X Marks the Region por Mitchell Cavanagh

Tanto los fanáticos como los escritores de ciencia ficción pasan incontables horas elaborando intrincados sistemas estelares, repletos de planetas, lunas y una colección de civilizaciones que viajan al espacio. El éxito de misiones como el Telescopio Espacial Kepler (en adelante Kepler) y el Satélite de Estudio de Exoplanetas en Tránsito (TESS) han demostrado que nuestro sistema solar es solo uno de los muchos sistemas de múltiples planetas presentes en la Vía Láctea. Sin embargo, nuestra capacidad para determinar con precisión la “arquitectura planetaria” (la configuración orbital de los planetas) de un sistema extrasolar dado es muy deficiente. Saber cómo se configuran los planetas en diferentes sistemas extrasolares ayudaría enormemente a comprender cómo se forman los planetas y cómo evolucionan los sistemas planetarios (por ejemplo, a través de la migración planetaria). Los exoplanetas son inherentemente difíciles de detectar. El medio principal para detectarlos consiste en medir la pequeña atenuación de una estrella a medida que un planeta se mueve frente a ella. Para comprender mejor los sistemas estelares, en lugar de considerar cada exoplaneta individualmente, podemos considerar toda la población de exoplanetas a la vez a través de la inferencia estadística. Recientemente, este método se ha vuelto viable gracias a la gran cantidad de datos de exoplanetas recolectados. El artículo de hoy presenta un marco estadístico: DYNAmical Multi-planet Injection TEster (DYNAMITE), diseñado para predecir la presencia de exoplanetas que hasta ahora han eludido la detección.

¡A cubierto!

El método central de DYNAMITE consiste en determinar la probabilidad de encontrar un planeta adicional en un sistema existente de varios planetas, basado en las estadísticas generales de una población representativa existente. Los autores consideran una función de densidad de probabilidad (PDF) combinada sobre la inclinación, el período orbital y el radio planetario, asumiendo que cada uno de estos parámetros tiene su propia distribución independiente. Cada una de estas PDF iniciales se generó con base en los datos de Kepler, con un rango de períodos orbitales restringidos de 0.5 a 730 días, radios planetarios de 0.5 a 5 radios de la Tierra e inclinaciones entre 0 y 180 grados. El Método de Montecarlo (este es un medio de aproximación de algo mediante muestreo aleatorio repetido) se utiliza para muestrear las distribuciones de probabilidad completas e “inyectar” nuevos planetas en el sistema. Para llegar a resultados acertados, el sistema planetario debe ser dinámicamente estable. Esta estabilidad depende de las órbitas de los planetas más internos y externos, sus masas y la masa de la estrella madre. Es difícil determinar con precisión las masas de exoplanetas a través del método de tránsito común, por lo que los autores utilizan una relación masa-radio para estimar las masas a partir de los radios planetarios.

Punto óptimo

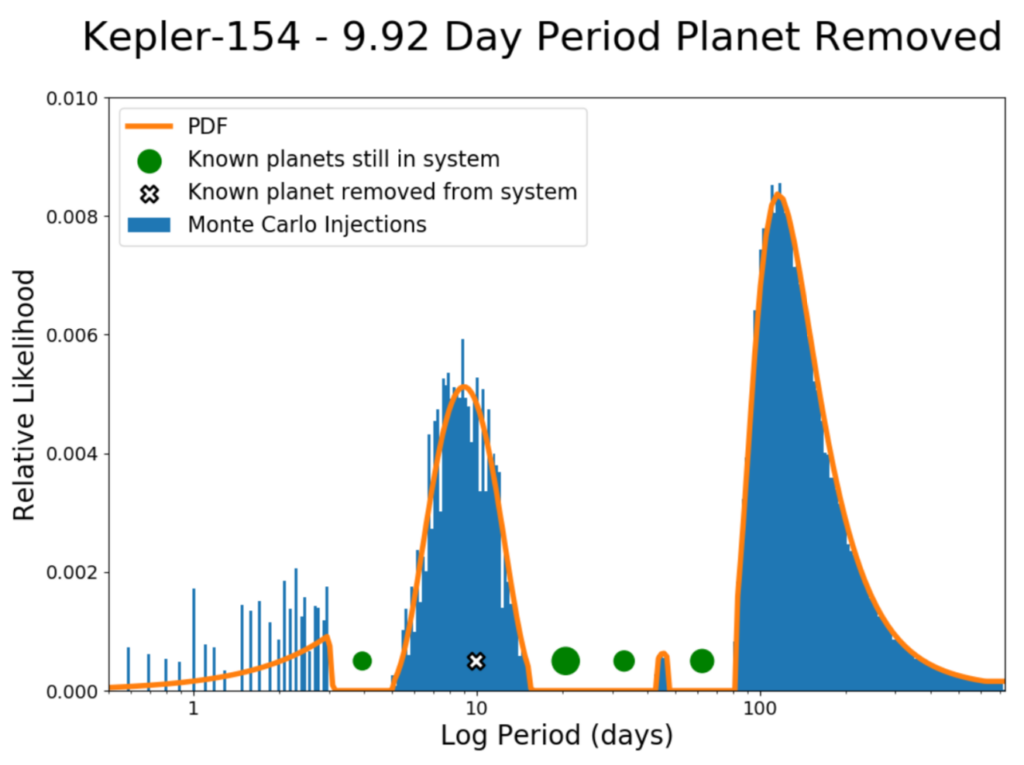
El modelo se sometió a pruebas rigurosas de poder estadístico y robustez. Varios escenarios de prueba incluyeron la eliminación de un planeta conocido para ver si el modelo podría reproducirlo, y la eliminación de un planeta mientras se alteran los planetas restantes. La Figura 1 muestra un ejemplo de la PDF en función del período orbital para el sistema Kepler-154 con el planeta conocido a P = 9.92 días (Kepler-154 f) eliminado. Del total de predicciones de Montecarlo que inyectan (o añaden) un nuevo planeta dentro de la órbita del planeta más externo, el 97% corresponde a la región del planeta removido. En cuanto al radio, el 67% de las predicciones de los modelos se encuentran dentro de tres desviaciones estándar, mientras que la propagación es más sustancial para la inclinación (43%). Las inyecciones medias coinciden bastante bien con los parámetros del planeta conocido (como en la Figura 1, donde el pico está justo por debajo del valor conocido para el período), pero los autores afirman que dado que DYNAMITE tiene como objetivo principal ayudar a guiar las observaciones futuras, no está diseñado para proporcionar predicciones exactas, sino más bien un rango probable de valores.

Ejecución especulativa

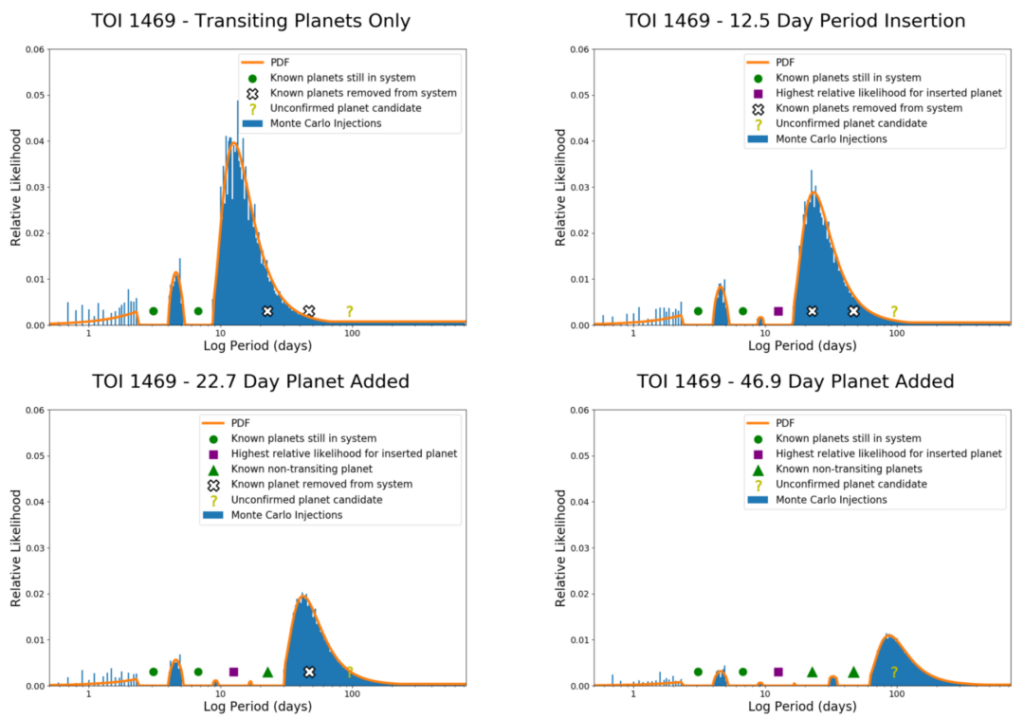
Una de las principales aplicaciones de DYNAMITE radica en el análisis de sistemas con planetas candidatos; planetas que se sospecha que están allí pero que aún no se han confirmado definitivamente. TOI 1469 se utiliza como ejemplo para ilustrar la naturaleza iterativa del modelo estadístico. La Figura 2 muestra las diversas etapas de DYNAMITE para el sistema TOI 1469 (HD 219134 / Gliese 892). Se sabe que este sistema tiene dos planetas en tránsito y al menos tres planetas que no están en tránsito. Comenzando con solo los dos planetas en tránsito conocidos, la PDF alcanza su punto máximo en alrededor de 12.5 días. Entonces, aquí se inserta un planeta y el modelo se ejecuta nuevamente. Ahora, la PDF alcanza su punto máximo cerca del planeta conocido alrededor de los 23 días (HD 219134 f tiene un período de 22.72 +/- 0.02 días), por lo que insertamos otro planeta aquí y ejecutamos el modelo nuevamente. Procediendo de esta manera, el modelo predice otro planeta a ~46 días (correspondiente a HD 219134 f con período orbital 46.86 +/- 0.03 días), mientras que en la última iteración el modelo predice un cuarto planeta a ~ 87 días, correspondiente a la planeta candidato no confirmado.

Al espacio de la probabilidad y más allá

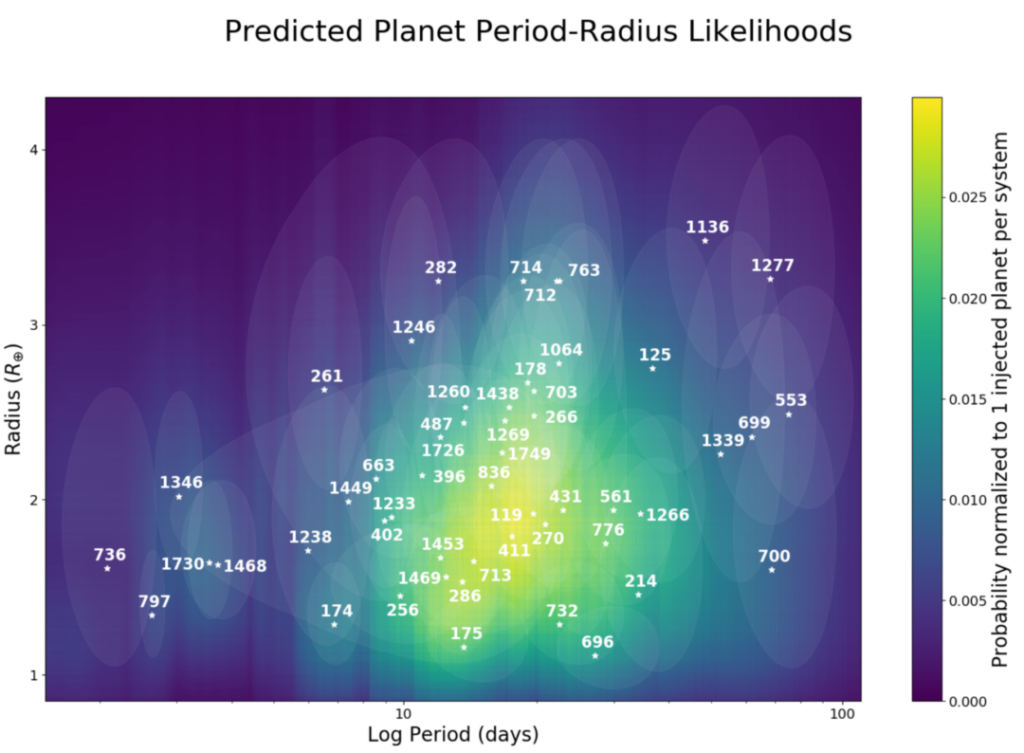
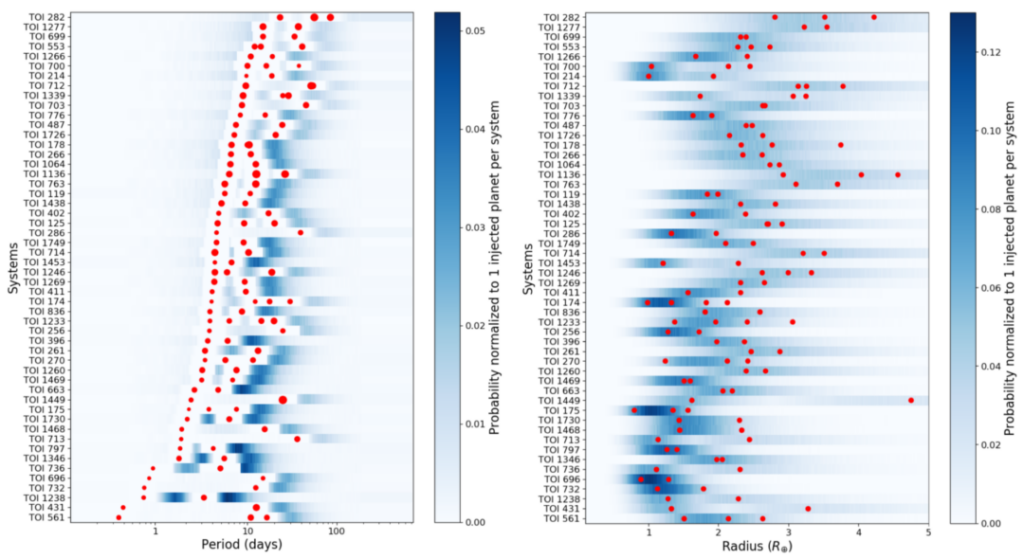
Otro propósito de DYNAMITE es analizar los sistemas multiestelares recientemente identificados descubiertos por TESS e identificar los sistemas con mayor probabilidad de contener planetas adicionales para que puedan ser inspeccionados nuevamente. Una muestra de sistemas multiestelares conocidos del archivo ExoFOP-TESS se probó con el modelo estadístico. La Figura 3 muestra los resultados generales del modelo utilizando el modelo de relación de períodos de Kepler, mientras que la Figura 4 muestra el PDF exacto para cada sistema TESS para el período orbital y el radio planetario.

Con la capacidad de predecir las ubicaciones de los planetas hasta ahora no detectados, las encuestas futuras pueden estar más enfocadas y dirigidas. Estudiar estos sistemas en detalle y confirmar si estos planetas adicionales están presentes o no, nos permite restringir y refinar modelos de arquitecturas planetarias, nuestro conocimiento de los mecanismos que rigen la evolución de los sistemas planetarios y, en última instancia, nuestra comprensión de cómo los exoplanetas formar.