¿Cómo se ve realmente una estrella de neutrones?

• Título del artículo: 1) The relativistic “looks” of a neutron star 2) Light Deflection Near Neutron Stars
• Autores: H.P. Nollert, H. Ruder, H. Herold and U. Krauss
• Institución del primer autor: Lehrstuhl für Theoretische Astrophysik, Universität Tübingen, Alemania
• Estado del artículo I: acceso abierto en arXiv aquí y aquí
• Astrobite original: What does a neutron star actually look like? por Lisa Drummond

Hoy estaremos viendo dos artículos que intentan responder a la pregunta planteada en el título: ¿cómo se ve de cerca una estrella de neutrones? En el proceso, ilustran (1) una característica interesante de la relatividad, lo que significa que podemos ver el lado lejano de una estrella de neutrones desde un punto de vista único y (2) que esta característica es relevante para comprender las observaciones astrofísicas.

En ausencia de un campo gravitatorio, las órbitas de fotones son sencillas: ¡viajan en línea recta! Sin embargo, en presencia de un campo gravitatorio fuerte, este ya no es el caso. Las fuerzas gravitacionales de un cuerpo masivo harán que la estructura del espacio a su alrededor se curve. Cuanto más denso sea el objeto, más se curvará el espacio-tiempo. Los fotones seguirán los contornos del espacio-tiempo y, por lo tanto, viajarán a lo largo de órbitas curvas.

Esto es cierto incluso para las estrellas que no son particularmente densas (como nuestro Sol). Aún habrá una pequeña desviación de la luz que viaja cerca del Sol debido a la curvatura del espacio-tiempo en esa región (ver Figura 1). Este efecto fue predicho por Einstein y medido con éxito en 1919. Esto se logró tomando fotografías de una región del cielo centrada en el Sol durante un eclipse solar total (el eclipse solar significaba que la posición de las estrellas en esa región eran visibles sin ser opacadas por la luz del Sol). Luego, se tomó otra fotografía de esas mismas estrellas cuando el Sol estaba lejos de esta área del cielo. Las dos fotografías se compararon y la conclusión fue que la luz se desvió, lo que confirma la predicción de la relatividad general.

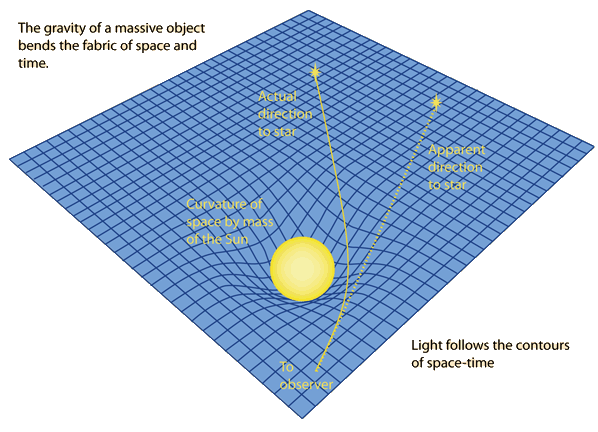
Figura 1: La gravedad del Sol dobla el espacio-tiempo a su alrededor. La luz seguirá a lo largo de la tela del espacio-tiempo curvada. A medida que la luz de una estrella de fondo pasa por el Sol, se desvía y, por lo tanto, la posición aparente de la estrella es diferente de la posición real de la estrella. (Fuente de la imagen: http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/grel.html)

El fotón orbita alrededor de una estrella de neutrones

Como en el caso del Sol, la gravedad alrededor de una estrella de neutrones hace que el espacio-tiempo se doble a su alrededor. Una estrella de neutrones contiene la masa del Sol comprimida en un objeto que es del tamaño de una ciudad. Por lo tanto, los efectos relativistas, como la desviación de la luz, serán incluso más pronunciados cerca de una estrella de neutrones en comparación con el Sol. Comprender las trayectorias de los fotones es crucial para determinar cómo será un objeto relativista, como una estrella de neutrones.

Usualmente pensamos que el espacio es tridimensional, es decir, se describe en términos de tres coordenadas, por ejemplo (x,y,z). Sin embargo, en la Relatividad General, necesitamos cuatro coordenadas, incluyendo el tiempo, es decir (x,y,z,t). Las cuatro coordenadas están estrechamente vinculadas; el valor de la cuarta coordenada (tiempo) tiene un efecto en las otras tres coordenadas, por lo tanto, lo necesitamos para una descripción completa de la geometría del espacio-tiempo.

Para un objeto con simetría esférica (lo cual es muy relevante en la astrofísica, donde los cuerpos gravitantes típicamente tendrán geometría esférica), la métrica de Schwarzschild describirá la curvatura del espacio-tiempo. Esta métrica nos dice cómo el espacio-tiempo se curvará cerca de una estrella de neutrones y, en particular, cómo cambiará la curvatura en función de la masa de la estrella de neutrones.

Si consideramos el movimiento ecuatorial de un fotón (es decir, solo nos preocupamos por las trayectorias a lo largo de un plano a través del ecuador de la estrella), entonces el movimiento del fotón se puede describir con tres coordenadas, (r,Φ,t) donde r y Φ son coordenadas polares (ver Figura 2).

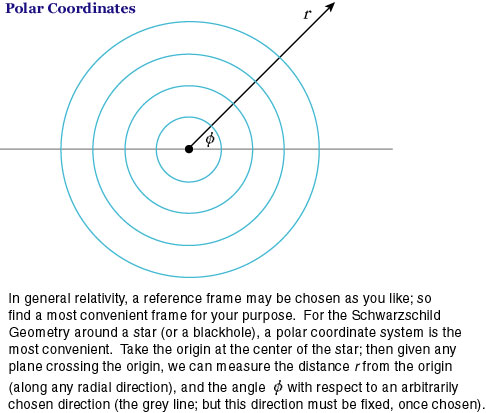
Figura 2: Las coordenadas polares describen la geometría de un corte ecuatorial a través de una estrella de neutrones. (Fuente de la imagen: http://www1.kcn.ne.jp/~h-uchii/schwarzschild.html)

Las ecuaciones de movimiento se pueden resolver numéricamente para encontrar la trayectoria de un fotón (es decir, la posición angular Φ del fotón en un radio particular r). Notamos que la trayectoria es una función del parámetro b que se llama el parámetro de impacto . El parámetro de impacto es la distancia del fotón desde una línea a través del centro de la estrella (ver Figura 3).

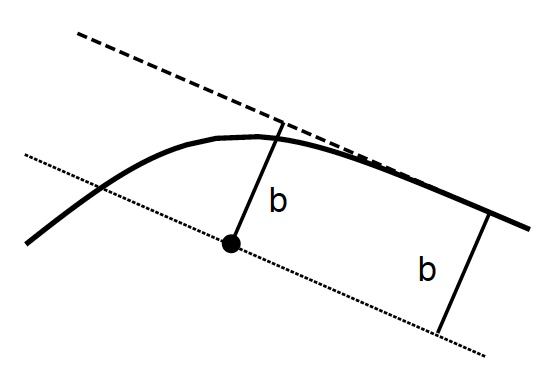
Figura 3: Esta figura muestra la definición del parámetro de impacto b. El punto negro corresponde al centro de la estrella de neutrones.

El valor del parámetro de impacto b determina qué tipo de movimiento ocurrirá alrededor de la estrella de neutrones. Hay dos regímenes diferentes: (1) b < b_c   y  (2) b > b_c  donde  b_c es el valor crítico del parámetro de impacto. A continuación se muestran algunos ejemplos de los dos tipos de órbitas para los dos regímenes en la Figura 4 y 5, respectivamente. Una cosa que notamos sobre el movimiento de los fotones en proximidad de una estrella de neutrones es que no solo pueden desviarse los fotones como en el caso de nuestro Sol, los fotones pueden caer en órbitas alrededor de la estrella de neutrones (ver Figura 4).

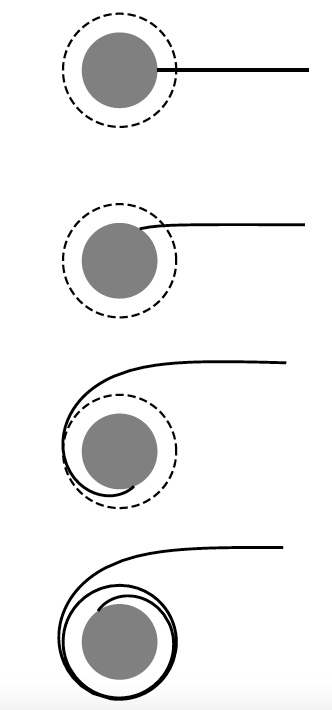
Figura 4: Órbitas de un fotón alrededor de una estrella de neutrones en el régimen b<b_c con b aumentando de arriba a abajo. (Crédito: Figura 2 en “Light Deflection Near Neutron Stars”)

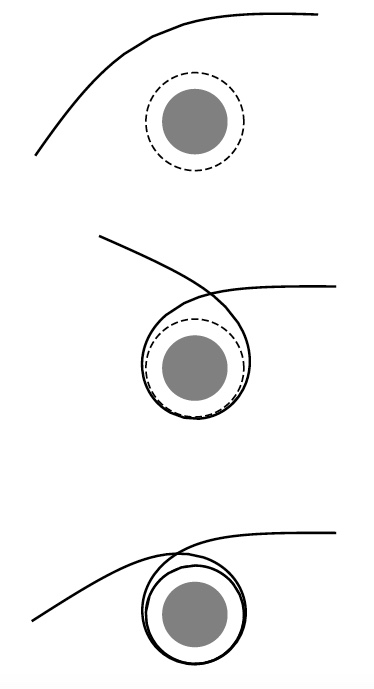
Figura 5: El fotón orbita alrededor de una estrella de neutrones en el régimen b> b_c, con b disminuyendo de arriba a abajo. (Crédito: Figura 3 en “Light Deflection Near Neutron Stars”)

Radiación de la superficie de la estrella de neutrones

Debido a la desviación extrema de los fotones alrededor de una estrella de neutrones, el aspecto de una estrella de neutrones es diferente a la realidad física. Nuestras mentes humanas se han adaptado a la gravedad de la Tierra y suponen que los caminos que toman todos los fotones son rectos. Esta no es una suposición válida en la superficie de una estrella de neutrones, donde las fuerzas gravitacionales son 2×10¹¹ veces más fuertes que en la Tierra.

La radiación emitida por la estrella de neutrones se curva de tal manera que partes de la superficie trasera (normalmente invisibles) se vuelven visibles (ver Figura 6). De hecho, es posible que los fotones queden atrapados a lo largo de una órbita (ver Figura 4), lo que hace que toda la superficie sea visible. La masa de un objeto determina su radio de Schwarzschild r_s. Un objeto con un radio más pequeño que su radio Schwarschild será un agujero negro. Por lo tanto, mientras más cercano esté el radio del objeto al radio de Schwarschild, más “agujero negro” será, y más espacio-tiempo se curvará a su alrededor.

Por lo tanto, la cantidad que determina la cuánta deflexión experimentará un fotón al viajar cerca de una estrella de neutrones es la relación del radio de Schwarzschild con el radio de la estrella de neutrones R/r_s . A medida que esta cantidad disminuye, se ve más y más de la superficie posterior de la estrella de neutrones, como se muestra en la Figura 6.

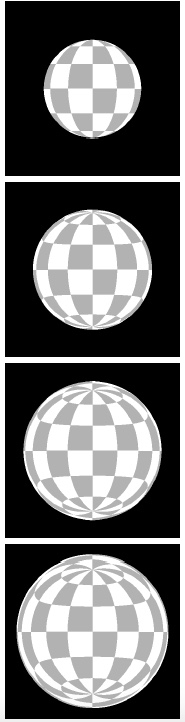
Figura 6: Cuatro imágenes de estrellas de neutrones con el mismo radio R pero con diferentes masas y, por lo tanto, diferentes r_s. La relación R / r_s disminuye de arriba a abajo. (Crédito: Figura 6 en “Light Deflection Near Neutron Stars”)

Perfiles de pulso de estrellas de neutrones

Comprender la desviación de la luz alrededor de las estrellas de neutrones es importante para determinar su perfil de pulso de rayos X. Este fenómeno se discute en detalle en este astrobite; los autores del astrobito de hoy resumen un modelo simple que discutiré brevemente aquí. En un binario de rayos X de acreción (que es una estrella de neutrones en un sistema binario que se acrecienta de su compañero de estrella no neutrónica), la materia se canaliza a lo largo de las líneas del campo magnético hacia los polos, donde la energía cinética se convierte en rayos X radiación. Observamos los pulsos regulares de esta radiación de rayos X a medida que gira la estrella de neutrones. Naturalmente, la radiación emitida cerca de los polos de la estrella de neutrones se verá afectada por la desviación de la luz debido a la relatividad general.

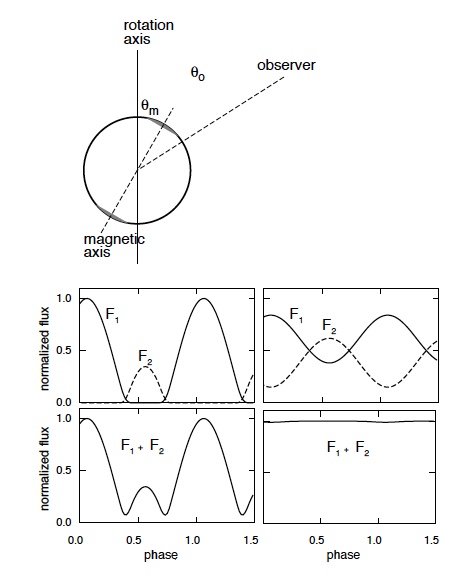
Figura 7: Perfiles de pulso de rayos X de un binario de rayos X de acrecentamiento para R / r_s = 2.4 (columna derecha) y R / r_s = ∞ (columna izquierda). F₁ corresponde al flujo de una de las tapas polares y F₂ corresponde al flujo de la otra tapa polar. F₁ + F₂ es el flujo de ambos casquetes polares combinados. Aumento de la deflexión del fotón (es decir, la disminución de R / r_s reduce la modulación en el flujo. (Crédito: Figura 12 en “Light Deflection Near Neutron Stars”)

La emisión de rayos X proviene de los polos de la estrella de neutrones. Sin ninguna desviación de la luz, ambos polos de la estrella de neutrones solo son visibles durante parte del período de la estrella de neutrones y desaparecen en otros momentos, por lo tanto, el flujo de rayos X se modulará a lo largo del período de la estrella de neutrones. Cuando  R/r_s  es pequeño (la estrella de neutrones es muy compacta), hay una desviación sustancial de la luz y, por lo tanto, casi toda la superficie de la estrella de neutrones es visible todo el tiempo. Debido a que ambos polos son visibles todo el tiempo, siempre vemos un flujo de rayos X. Esto significa que esencialmente no habrá modulación de flujo cuando  R/r_s  sea pequeño, como se ve en la Figura 7.

La relatividad no es simplemente un bloque de construcción vital de la física teórica fundamental, juega un papel directo en la astrofísica observacional. Podemos usarlo para comprender la radiación que recibimos de objetos extremos y compactos, como las estrellas de neutrones, e incluso aprender más sobre el contenido misterioso de sus interiores.