- Título: The Exomoon Corridor: Half of all exomoons exhibit TTV frequencies within a narrow window due to aliasing
- Autores: David Kipping
- Institución del primer autor: Departmento de Astronomía, Universidad de Columbia
- Estado: Publicado el 04 de noviembre de 2020 en MNRAS de acceso abierto en arXiv
Siguiendo el legado de Galileo en otros sistemas planetarios
Nuestro sistema solar albergar más de 200 satelites naturales, o lunas, que orbitan a distintos planetas. Jupiter y Saturno son los planetas con más lunas, 79 y 82, respectivamente. En base a esta información es lógico esperar que planetas en otros sistemas solares, o exoplanetas, tengan lunas, denominadas exolunas (en inglés exomoons). En contraste al descubrimiento de las principales lunas de Júpiter por Galileo, los telescopios actuales no permiten la detección directa (visual) de estos cuerpos celestes. Sin embargo, los exoplanetólogos han desarrollado métodos para inferir la presencia de exolunas por su efecto en la orbita del planeta anfitrión.
Cronómetrando exoplanetas
El método más prometedor para descubrir exolunas consiste en identificar desviaciones del tiempo exacto del tránsito de un exoplaneta (Variación de Tiempo de Tránsito o TTV, por sus siglas en inglés). Recordamos que los tránsitos son eventos que podemos observar en algunos sistemas planetarios cuando el planeta bloquea parte de la luz de la estrella al cruzar nuestra linea de visión. A causa de la atracción gravitatoria de las exolunas, las orbitas de sus exoplanetas sufren ligeras variaciones, provocando que sus tránsitos se produzcan un poco antes o un poco despues.
Este mismo método ha sido empleado para descubrir otros planetas en el mismo sistema dado que también producen TTVs. Precísamente esto presenta un obstáculo para discernir los TTVs causados por exolunas.
Venciendo al submuestreo
Un problema intrínseco al estudiar las TTVs es el hecho de que el período de la luna alrededor del planeta es menor al del planeta alrededor de la estrella. Es decir, podemos observar un tránsito del planeta una vez cada un período orbital (365 días para la Tierra, o un año), sin embargo, su luna habrá realizado numerosas revoluciones alrededor del planeta (en el caso de la Luna-Tierra, unas 13 veces). Esto resulta en un submuestreo (en inglés undersampling) que impide conocer el verdadero período de la luna alrededor del planeta.
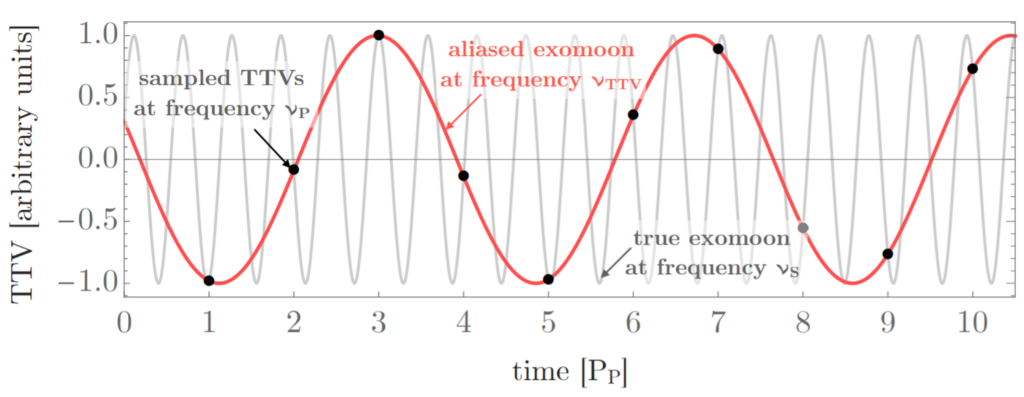
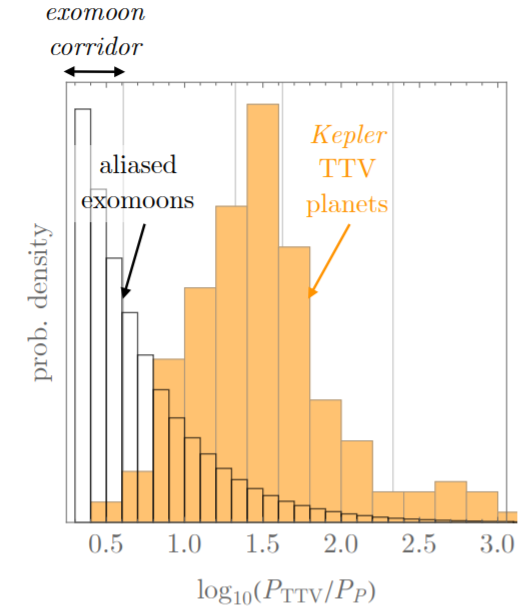
El Professor Kipping desarrolla un modelo que le permite obtener el verdadero período orbtial de las exolunas a partir de los períodos observados (con submuestreo). En el presente artículo expone los resultados de simular una población de exolunas con distintos parámetros (separación del planeta, frecuencia de submuestreo) para demostrar que el 50% de todas las exolunas induce TTVs con un período de 2 a 4 ciclos (períodos orbitales del planeta). Este rango de valores lo denomina cómo exomoon corridor (corredor de exolunas) por su visualización gráfica en la Figura 2.
Para poner en práctica los resultados obtenidos, el autor analiza el candidato a exoluna más prominente hasta la fecha: Kepler-1625b. Utilizando los cuatro tránsitos observados en el pasado, se obtiene un período de TTV de 4.4 ciclos para Kepler-1625b I, cercano a la media de 4 ciclos deducida en el apartado anterior.
Conclusiones
Los argumentos expuestos en este artículo muestran que las exolunas manifiestan su presencia a través de períodos de TTV más largos que los intrínsecos. Convertir estos períodos observados a los reales no es una tarea fácil porque no tiene una solución única. Sin embargo, las simulaciones nos permiten afirmar que el 50% de todas las exolunas exhibe un período de TTV en el rango de 2 a 4 períodos. Con esto podemos identificar candidatos de manera inmediata para análisis posteriores. Un análisis más profundo es necesario para confirmar la presencia de una exoluna, este criterio es el primer paso para reconocer a los candidatos más prometedores.
Comentarios
Aún no hay comentarios.