Analizando las ondas gravitacionales con principios de física básica

• Título:  An analysis of the LIGO discovery based on Introductory Physics
• Autores: H. Mathur, K. Brown & Ashton Lowenstein 
• Institución del primer autor: Case Western Reserve University

Hace unos meses, el consorcio LIGO anunció por primera vez la detección de perturbaciones en el espacio-tiempo producidas por la fusión de dos agujeros negros. Estas perturbaciones, llamadas ondas gravitacionales, son como pequeños “terremotos” en el espacio-tiempo y su existencia había sido predicha por la teoría de la relatividad general hace aproximadamente cien años. Detectar estas perturbaciones nos permite no sólo poner a prueba la teoría de Einstein, sino también aprender más sobre la frecuencia y la física de las fusiones de agujeros negros. En este astrobito, describimos hace unos meses cómo fueron llevadas a cabo las mediciones y sus implicaciones astrofísicas. El paper que discutimos hoy explica el descubrimiento de LIGO usando conceptos básicos de física de primer año.

Recordemos cómo se midieron las ondas gravitacionales por primera vez. El experimento LIGO funciona como un interferómetro de Michelson, cuya configuración de láseres y espejos permite medir distancias con mucha precisión. Cuando las ondas gravitacionales atraviesan el experimento, se genera una perturbación en su configuración y un patrón de interferencia de las ondas de luz láser.  Este patrón puede traducirse a una “tensión” y frecuencia de las ondas gravitacionales como función del tiempo, lo que se muestra en la Figura 1.

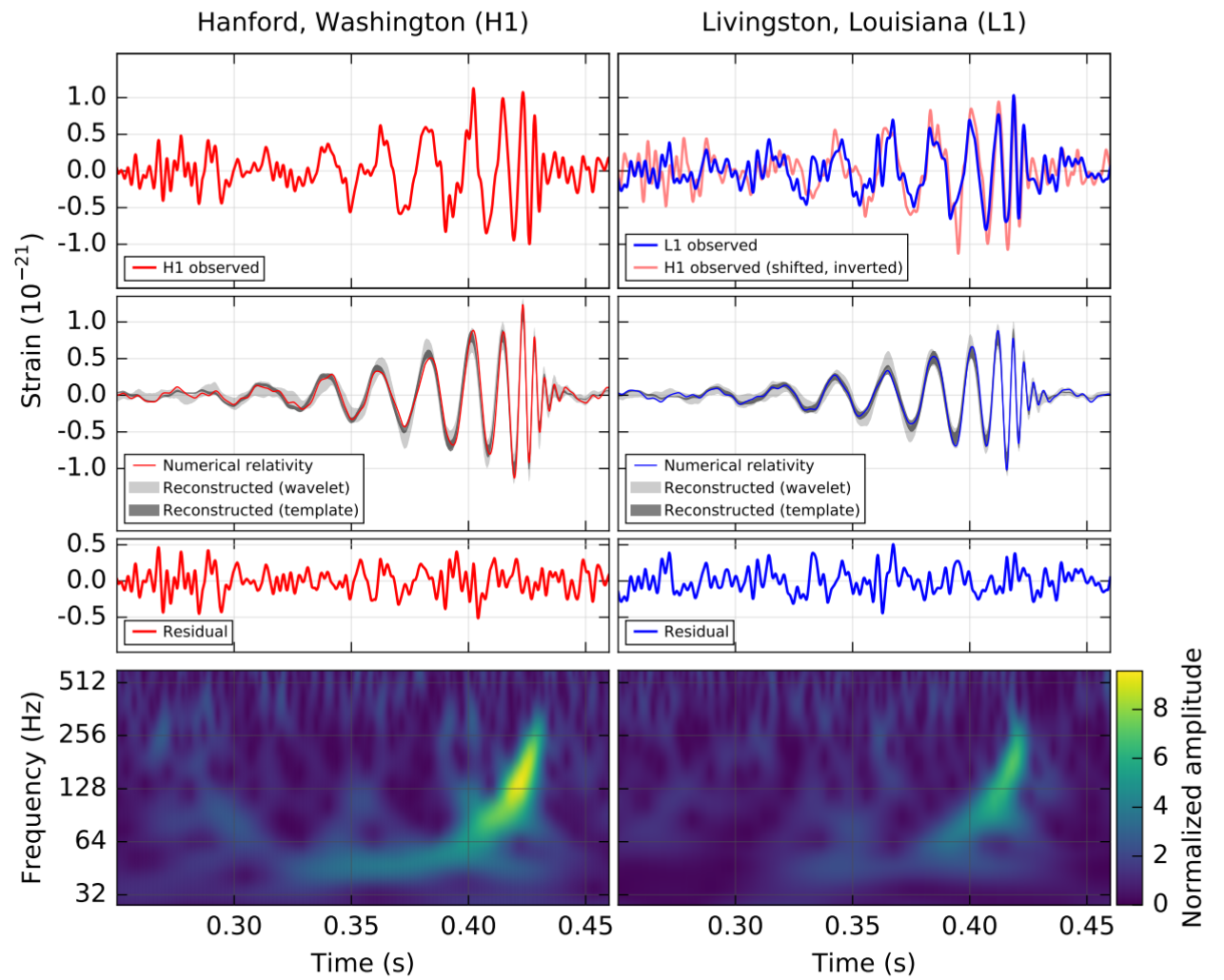
Figura 1.  La fuente de ondas GW150914 observada por el detector en Hanford (izquierda) y en Livingston (derecha). La fila superior muestra la “tensión” producida por las ondas gravitacionales y medida por cada detector. La segunda fila muestra la tensión en la banda de 35-350 Hz  (quitando bajas y altas frecuencias), una forma de onda de relatividad numérica para un sistema consistente con los parámetros del sistema de agujeros negros (línea sólida), y regiones de 90% de confianza para la reconstrucción independiente de las dos formas de onda (en gris). La tercera fila muestra el ruido residual luego de substraer la forma de onda del modelo numérico. La última fila muestra la tensión medida en el plano tiempo-frecuencia, con un distintivo “chirp” correspondiente a un incremento de la frecuencia con el tiempo. Figura 1 del manuscrito que anuncia la detección. 

Supongamos que ésta señal es generada por la fusión de dos agujeros negros de masas puntuales M y m. Veamos qué podemos aprender acerca de éste sistema usando la Figura 1 y un poco de física de primer año. Primero, imaginemos que los dos agujeros negros se desplazan en órbitas circulates alrededor del centro de masa del sistema, con radios orbitales R y r respectivamente. La tercera ley de Kepler permite relacionar la frecuencia orbital (w, inversamente proporcional al tiempo que lleva completar una órbita), con el radio orbital, a través de (Ec. 1):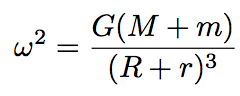La energía total del sistema está dada por la suma de la energía potential y la energía cinética de las dos masas puntuales. Queremos determinar cómo depende la energía del sistema con respecto a R+r, para esto podemos directamente usar la ecuación anterior y obtener una relación entre la energía total y la frecuencia orbital:

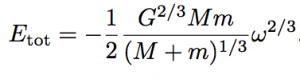
Ahora bien, si la física fuera la de Newton, los agujeros negros continuarían orbitando el centro de masa común por la eternidad. En la relatividad general, en cambio, este sistema “radía” energía gravitatoria.  Digamos que los agujeros negros se cansan con el tiempo, y sus órbitas se van reduciendo. ¿A dónde va la energía perdida? En verdad, esta energía no se pierde, sino que se transforma en el “movimiento sísmico” del espacio-tiempo, y una pequeña porción de ella se invierte en perturbar el interferómetro de LIGO, generando los patrones de la Figura 1. Puedes ver una interpretación artística de éste proceso en la Figura 2.

Figura 2. Una visión artística de dos agujeros negros cuyas órbitas decaen con el tiempo. Las ondas irradiadas son perturbaciones del espacio-tiempo que eventualmente pueden ser detectadas por LIGO en la tierra. Crédito: LIGO/T. Pyle.

¿Cómo podemos saber cuánta energía se emite? Por un lado, podemos tomar la derivada temporal de la expresión que escribimos más arriba para obtener la potencia. Por otro lado, podemos imaginar que el cambio de energía debe estar relacionado con:  la distribución de masa del sistema, la frecuencia de la órbita, la constante de Newton (G) y la velocidad de la luz (c). La distribución de masa está codificada en el momento de inercia del sistema (I). No hay muchas maneras de combinar estos parámetros para obtener una cantidad que tenga unidades de energía por unidad de tiempo. Con un poco de análisis dimensional, obtenemos:

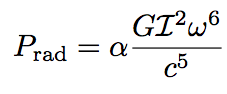
Como hemos obtenido este resultado por análisis de las unidades de las variables involucradas, no podemos saber cuánto vale α. Normalmente, aquí asumiríamos que es un parámetro de orden ~1. Si hiciésemos la cuenta formalmente, usando relatividad general, descubriríamos que α=32/5. Balanceemos ahora las dos expresiones obtenidas para la potencia. El resultado es

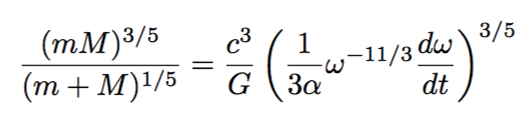
Ya estamos listos para abordar los datos. Sabemos ahora que el lado derecho de la expresión anterior se puede obtener a partir de las mediciones de LIGO: la Figura 1 nos nuestra la frecuencia de las ondas gravitacionales y cómo cambian con el tiempo. Esto nos permite obtener una estimación para el lado izquierdo. Pero más aún, esta expresión nos dice que si los agujeros negros se fusionan rápidamente, la frecuencia de la radiación emitida aumenta. (En verdad, la frecuencia de las ondas gravitacionales es el doble de la frecuencia orbital.) Usando esta última expresión y los datos que se ven en la Figura 1, los autores estiman que el lado izquierdo vale alrededor de 35 masas solares.

Pero ¿cómo pueden distinguirse las masas de cada agujero negro? Los agujeros negros se fusionan cuando su separación es igual a la suma de sus tamaños. Pensemos ahora en la definición de un agujero negro: es un objeto del cual la luz no puede escapar debido a la atracción gravitatoria. Sabemos que para cualquier esfera de masa M, existe una velocidad de escape mínima que se debe alcanzar para vencer la atracción gravitatoria. En el caso del agujero negro, la velocidad de escape es la velocidad de la luz, c. Por ende, escribiendo la velocidad de escape de una partícula en la vecindad de un agujero esférico, es posible estimar su radio:

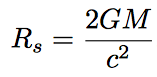
Cuando dos agujeros negros se fusionan, forman un nuevo agujero negro cuya masa es aproximadamente la suma M+m. El tamaño estimado del nuevo objeto será correspondientemente R+r. Ahora bien, examinemos nuevamente la ecuación (1). Si al momento de fusionarse, la órbita tiene un tamaño R+r, éste corresponderá a una frecuencia orbital crítica, que llamaremos la frecuencia de “chirp”:

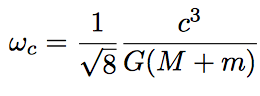
Ésta es (el doble de) la máxima frecuencia observada por LIGO en la Figura 1, ~300 Hz, y corresponde a las últimas ondas gravitacionales emitidas antes de que los agujeros se fusionaran. Eso nos permite estimar M+m en 76 masas solares. Usando esta estimación y la de la masa de “chirp”, podemos hallar M y m por separado, obteniendo M~53 y m~23 masas solares. ¡Nada mal! Un análisis completamente relativista, como el de LIGO, arroja M~36 y m~29 masas solares.

Recordemos algunas implicaciones del descubrimiento de LIGO y entendamos qué nos dicen los números que acabamos de calcular:

• La detección de LIGO se trata de la primera vez que se halla evidencia directa de la existencia de ondas gravitacionales. (Evidencia previa, pero indirecta, fue arrojada por el estudio de la órbita de púlsares binarios, que también decae por la emisión de ondas gravitacionales.)
• Esta detección nos permite hacer confrontaciones de la teoría de la relatividad general y ponerla a prueba como nunca antes.
• Nos informa que existen agujeros negros de ~30 masas solares y nos dice que sus fusiones probablemente sean frecuentes. Esto nos permitirá construir mejores modelos de evolución estelar.

El paper de Mathur et al. propone algunos cálculos y problemas adicionales, ¿te animas a resolverlos?